The method chosen for implementing Huygens' principle in FARSITE was developed by G.D. Richards (1990). His differential equation solves for the spread vector (rate and direction) of each point knowing its orientation on the fire perimeter and the heading, flanking, and backing dimensions of an elliptical fire originating at that point. The elliptical dimensions are obtained from empirical models for the length to width ratio determined by the wind-slope vector (Anderson 1983, Alexander 1985). These dimensions are given units of fire spread rate from the predicted rate of forward spread (Rothermel 1972). The calculated spread rates are then multiplied by the time-step to obtain the positions of all points on the fire front at the end of the time-step.
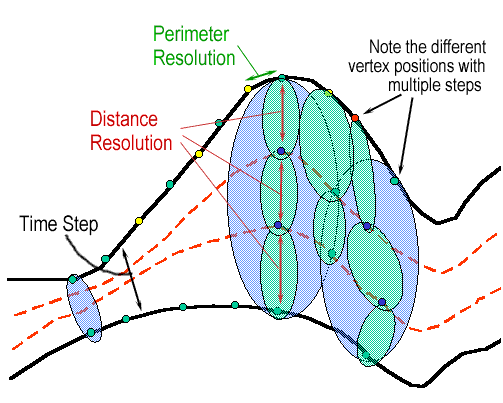
Several modifications to this procedure are used in FARSITE to increase control over the simulation. The most important change is the concept of a dynamic time-step that is implemented through distance checking. Distance checking ensures the spread distance of any point on a fire is less than the maximum distance in a given time step. Without this procedure, there would be no control over the amount of spatial information used by the simulation. Faster moving heading portions of a fire would automatically use a coarser scale of landscape information than slower portions of a fire; important landscape information within a time step such as a river or change in fuel type could be ignored. Distance checking allows control over the minimum level of spatial detail used in a simulation.
When you are simulating multiple fires at a time, Farsite uses the fastest moving point on each fire independently to regulate the growth of that fire front. With distance checking on each fire, slow moving fires can accomplish their growth in one calculation per sub time-step while faster moving fires may take several steps. Merging is accomplished after the end of the actual time step. With simulation-level distance checking, the same internal time step used for all fire fronts (determined by the fastest vertex among all fronts) and merging can then be accomplished many times per actual time step.
During distance checking, the working value or internal value of the time step is constantly changing. If during a time step the distance check is exceeded by any point on a fire, the minimum time from all points to spread that distance is used as the new time step. The original time step is then decreased by that amount, and the process repeated until the original time step is consumed. The time step then becomes important only as a consistent interval for:
computing and displaying fire perimeters at meaningful time periods,
merging of multiple fire fronts, and
iterating the descent of embers.

In Richards (1990) application of his differential equation, he uses a single correcting iteration to compensate for the changing orientation of each point after a given time step. The orientation of each point on the fire front is a required input to the equation, but is changed as a result of the solution. Thus, an average orientation from the two time steps is used for each point in a second and final round of computations. This process can be repeated more often within a time step if greater averaging of the orientation is desired. At present, no correcting iterations are performed in FARSITE. This will be an area of further investigation as an option for the simulation.